Halo, teman-teman CYDUK Lovers. Bagaimana kabarnya? Semoga teman-teman semua dalam keadaan sehat dimanapun teman-teman berada. Disini, CYDUK Lovers akan membawakan sebuah materi yang cukup populer di kelas X IPA khususnya pada pelajaran Matematika. Materi apakah itu? Ya benar, disini CYDUK Lovers akan membahas materi tentang Vektor.
Teman-teman pasti sudah tidak asing lagi dengan Vektor, materi yang dipelajari ketika memasuki jenjang SMA. Sebenarnya pada pelajaran Fisika juga terdapat materi Vektor, namun ada sedikit perbedaan antara Vektor Fisika dan Vektor Matematika walaupun konsep keduanya sama. Nah pada kesempatan kali ini, CYDUK Lovers akan membahas materi Vektor pada pelajaran Matematika.
A. Pengertian Vektor
Vektor adalah besaran yang mempunyai besar dan arah. Dalam matematika vektor digambarkan dalam bentuk garis lurus yang mempunyai panjang dan arah.
B. Penulisan Vektor
āa
Penulisan nama vektor dapat ditulis sebagai berikut :
āa
Penulisan nama vektor dapat ditulis sebagai berikut :
- Pertama, dengan menggunakan huruf kapital harus menggunakan dua huruf, sebagai contoh vektor adalah vektor yang panjangnya sama dengan panjang ruas garis AB dan arahnya dariA ke B.
- Kedua, dengan huruf kecil hanya satu huruf, sebagai contoh .
C. Rumus Vektor
1. Vektor satuan

2. Besar panjang vektor

3. Penjumlahan/pengurangan vektor
.PNG)
4. Gambar proyeksi vektor a pada b

5. Proyeksi orthogonal skalar

6. Proyeksi orthogonal vektor

7. Titik p pembagi AB dengan perbandingan m:n

8. Sudut vektor

http://nuurilqolbii.blogspot.co.id/2013/02/rumus-rumus-vektor-matematika.html
D. Macam-macam Vektor
AB + BC = AC
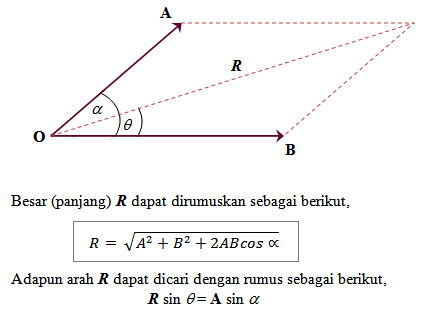
2. Metode Jajar Genjang
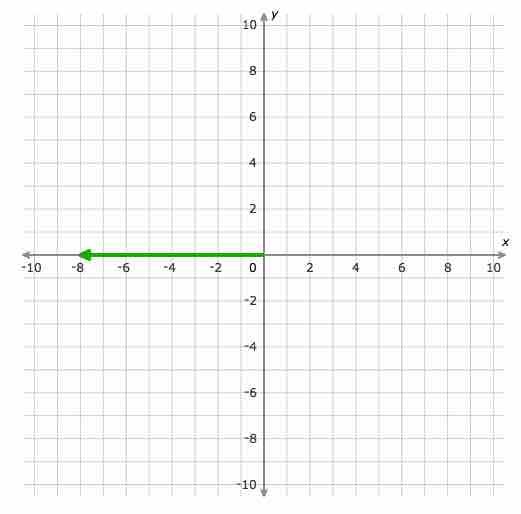 Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.
Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.
3. Diketahui vektor-vektor
4. Jika vektor
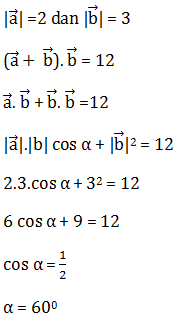
5. Diketahui

1. Vektor satuan

2. Besar panjang vektor

3. Penjumlahan/pengurangan vektor
.PNG)
4. Gambar proyeksi vektor a pada b

5. Proyeksi orthogonal skalar

6. Proyeksi orthogonal vektor

7. Titik p pembagi AB dengan perbandingan m:n

8. Sudut vektor

http://nuurilqolbii.blogspot.co.id/2013/02/rumus-rumus-vektor-matematika.html
D. Macam-macam Vektor
- Vektor nol
Vektor yang titik awal dan titik ujungnya sama (berimpit) disebut Vektor nol , seperti : AA = 0,vektor nol ini mempunyai panjang nool dan arah tak tentu.Contoh dala kehidupa sehari- harinya , seperti kita pergi ke sekolah dari rumah ,lalu kita kembali lagi ke rumah B. Macam-macam Vektor
- Vektor satuan
Sebuah vektor yang panjangnya satu dan dinotasikan sebagai e. Hal ini berarti |e| = 1 .Vektor satuan dari vektor r dinyatakan oleh

E. Operasi Vektor

E. Operasi Vektor
- Penjumlahan
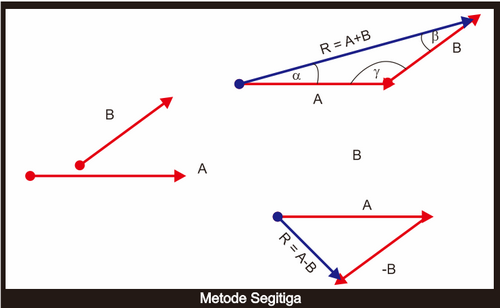
- Metode Segitiga
AB + BC = AC
2. Metode Jajar Genjang

3. Perkalian Skalar dengan Vektor
Bila k adalah sebuah skalar maka perkalian dengan vektor a dinyatakan dengan k a, sebuah vektor yang searah dengan a dan panjangnya k kali panjang a
4. Sifat-sifat skalar dengan vektor
4. Pengurangan Vektor
Pengurangan vektor sama dengan penjumlahan vektor dengan salah satu vektor negatif dari vektor semula.
Untuk memudahkan dalam operasi geometri, bentuknya sebagai berikut : perhatikan arah anak panahnya
CONTOH SOAL :
1. Temukan besarnya vektor. Tulis jawaban Anda dalam bentuk yang disederhanakan:
 Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.
Jawaban: 8. Penjelasan: untuk menemukan besarnya vektor, pertama cari titik awalnya di dasar panah dan titik terminalnya di ujung panah. Titik awalnya adalah (0,0) dan titik terminalnya adalah (-8,0). Karena koordinat y dari titik awal (0,0) dan titik terminal (-8,0) sama, vektornya horizontal. Jadi, besarnya adalah nilai absolut dari perbedaan koordinat x, yaitu | -8-0 | = 8.2. Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…
A. u.v = | w |
B. 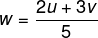
C. | u-w | = | v |
D. u – v tegak lurus w E. u + v tegak lurus w
Pembahasan:
Diketahui: | v – w | = | u – w | Kedua sisi di akarkan ^2}=\sqrt{(u-w)^2}) v.v + w.w – 2v.w = u.u + w.w – 2 u.w |v|2 + |w|2 – 2v.w = |u|2 + |w|2 – 2u.w
v.v + w.w – 2v.w = u.u + w.w – 2 u.w |v|2 + |w|2 – 2v.w = |u|2 + |w|2 – 2u.w
Dari soal diketahui | u | = | v | maka v.w = u.w u.w – v.w = 0 (u.w).w = 0 Karena perkaliannya = 0 maka (u-v) tegak lurus w.
Jawaban: D
3. Diketahui vektor-vektor 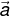 = (2, 2, z),
= (2, 2, z), 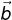 = (-8, y, -5) ,
= (-8, y, -5) , 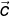 = (x, 4y, 4) dan
= (x, 4y, 4) dan 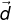 = (2x, 22, -z, 8). Jika vektor
= (2x, 22, -z, 8). Jika vektor 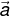 tegak lurus dengan vektor
tegak lurus dengan vektor 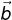 dan vektor
dan vektor 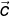 sejajar dengan
sejajar dengan 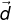 maka (y+z) =
maka (y+z) =
A. -5
B. -1
C. 1
D. 2
E. 5
B. -1
C. 1
D. 2
E. 5
Jawaban: C
4. Jika vektor 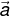 dan
dan 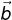 merupakan (
merupakan (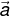 +
+ 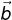 ).
).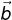 = 12 , |
= 12 , |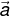 | = 2 dan |
| = 2 dan |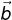 | = 3 maka sudut antara
| = 3 maka sudut antara 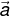 dan
dan 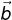 adalah….
adalah….
A. 60°
B. 45°
C. 300D. 250E. 200
B. 45°
C. 300D. 250E. 200
Pembahasan:
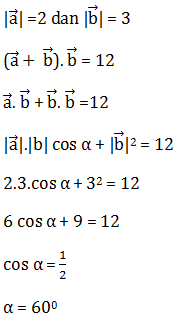
Jawaban: A
5. Diketahui 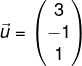 dan vektor
dan vektor 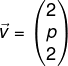 . Jika proyeksi skalar orthogonal
. Jika proyeksi skalar orthogonal  pada arah vektor
pada arah vektor 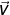 sama dengan setengah panjang vektor
sama dengan setengah panjang vektor 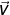 maka nilai p = …
maka nilai p = …
A. -4 atau -2
B. -4 atau 2
C. 4 atau -2
D. 8 atau -1
E. -8 atau 1
B. -4 atau 2
C. 4 atau -2
D. 8 atau -1
E. -8 atau 1
Pembahasan:

Jawaban: B
Source : https://www.pinterpandai.com/rumus-vektor-spasial-contoh-soal-jawaban/
SOAL LATIHAN :
- Diketahui a = t i - 8 j + h k dan b = (t +2) i + 4 j + 2 k. Jika a = - b maka vektor a dapat dinyatakan ...
A. i + 8j + 2 k
B. i + 8 j - 2k
C. i - 8j + 2k
D. - i - 8j + 2k
E. - i - 8j - 2k - Jika vektor a = 10i + 6 j - 3k dan b = 8 i + 3 j + 3k serta c = a - b, maka vektor satuan yang searah denga c adalah...
A. 6/7 i + 2/7 j + 3/7 k
B. 2/7 i + 3/7 j - 6/7 k
C. 2/7 i - 3/7 j + 6/7 k
D. 6/7 i - 3/7 j - 2/j k
E. -2/7 i + 6/7 j - 3/7 k - Diketahui titik-titik A (2, 5, 2), B (3, 2, -1), C (2, 2, 2). Jika a = AB dan b = CA dan c = b - a maka vektor c adalah...
A. (1,5,3)
B. (-1,5,3)
C. (-1,0,3)
D. (-1,3,5)
E. (-1,-3,5) - Diketahui U = 3 i + 2 j + k dan v = 2i + j dimana W = 3 U - 4 V maka besar W =...
A. √5
B. √7
C. √11
D. √13
E. √14 - Diketahui vektor u = 2 i - 3 j + 5 k dan v = - 3 i - 5 j + 2 k menga[it sudut Ɵ. Maka nilai tan Ɵ adalah...
A. √2
B. √3
C. √5
D. √6
E. 1 - Jika vektor u dan vektor v membentuk sudut 60 derajat dimana IuI = 4 dan IvI = 2, maka u (v + u) =A. 13B. 15C. 17D. 19E. 20
- Diketahui titik-titik A (3,-1,0), B(2,4,1) dan C(1.0,5). Maka panjang proyeksi vektor AB pada vektor BC adalah...A. 1/5 √30B. 2/5 √30C. 3/5 √30D. 4/5 √30E. √30
- Vektor-vektor u = 2i - mj + k dan v = 5i + j - 2k saling tegak lurus. Maka harga m haruslah...A. 2B. 4C. 6D. 8E. 10
- Diketahui D adalah titik berat segitiga ABC dimana A(2,3,-2), B(-4,1,2) dan C(8,5,-3). Maka panjang vektor posisi d sama dengan:A. 1B. 2C. √5D. √10E. √14
- Jika titik-titik P, Q, R segaris dan P(-1,1) dan R (3,5) dan PQ = QR maka titik Q adalah...A. (3,1)B. (1,3)C. (1,1)D. (3,3)E. (-3,-1)
KUNCI JAWABAN :
- a = - b maka t i - 8 j + h k = - (t +2) i - 4 j - 2 k
t = - (t +2)
t = - t - 2
2t = -2
t = -1
lalu h = -2
sehingga, a = - i - 8 j - 2 k
Jawaban: E - c = a - b = (10 i + 6 j - 3k) - (8i + 3 j + 3k) = 2 i + 3j - 6k
Sehingga
Maka vektor yang searah dengan c adalah
c = (2, 3, -6) / 7 atau c = 2/7 i + 3/7 j - 6/7 k
Jawaban: B - a = AB = B - A = (3,2,-1) - (2,5,2) = (1,-3,-3)
b = CA = A - C = (2,2,2) - (2,5,2) = (0,-3,0)
c = b - a = (0,-3,0) - (1,-3,-3) = (-1,0,3)
Jawaban:C - W = 3 (3 i + 2 j + k) - 4 (2i + j) = i + 2j + 3k

Jawaban: E -
Jadi Ɵ = 60 derajatSehingga tan Ɵ = tan 60 = √3Jawaban: B
- u (v + u) = u . v + u2 = IuI IvI cos 60 + u2= 4 . 2 . 1/2 + 42
= 4 + 16 =20Jawaban:E - u tegak lurus v maka:u . v = 0(2i - mj + k) (5i + j - 2k) = 10 - m - 2 = 0m =8Jawaban:D
- PQ = QR maka Q - R = R - Q2Q = R + PQ = 1/2 (R + P)Q = 1/2 (3,5) + (-1,1) = 1/2 (2,6) = (1,3)Jawaban: B









0 komentar:
Posting Komentar